Empuje

Empuje

•Empuje•

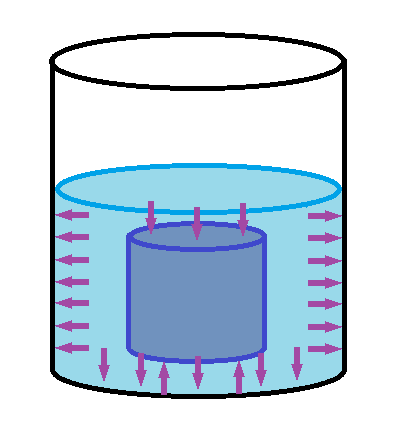
“Todo cuerpo sumergido en un fluido experimenta una fuerza hacia arriba igual al peso del volumen de fluido desplazado por dicho cuerpo”.

Arquímedes

El segundo principio importante de la estática de fluidos fue descubierto por el matemático y filósofo griego Arquímedes. La mayoría de las veces se aplica al comportamiento de los objetos en agua, y explica por qué los objetos flotan y se hunden y por qué parecen ser más ligeros en este medio. El concepto clave de este principio es el ‘empuje’, que es la fuerza que actúa hacia arriba reduciendo el peso aparente del objeto cuando éste se encuentra en el agua.

El principio de Arquímedes permite determinar la densidad de un objeto cuya forma es tan irregular que su volumen no puede medirse directamente. Si el objeto se pesa primero en el aire y luego en el agua, la diferencia de peso será igual al peso del volumen de agua desplazado, y este volumen es igual al volumen del objeto, si éste está totalmente sumergido. Así puede determinarse fácilmente la densidad del objeto.

Principio de Arquímedes

Al sumergirse parcial o totalmente en un fluido, un objeto es sometido a una fuerza hacia arriba, o empuje. El empuje es igual al peso del fluido desplazado. Aquí se ilustra el principio en el caso de un bloque de aluminio y uno de madera. (1) El peso aparente de un bloque de aluminio sumergido en agua se ve reducido en una cantidad igual al peso del agua desplazada. (2) Si un bloque de madera está completamente sumergido en agua, el empuje es mayor que el peso de la madera (esto se debe a que la madera es menos densa que el agua, por lo que el peso de la madera es menor que el peso del mismo volumen de agua). Por tanto, el bloque asciende y emerge del agua parcialmente —desplazando así menos agua— hasta que el empuje iguala exactamente el peso del bloque.

La fórmula para calcular el empuje es la siguiente:

 

Donde:

E=empuje                                                                                                                                            r= densidad de la sustancia que provoca el empuje(^kg/_m³)                                                                                                             g= aceleración de la gravedad                                                                                                         v= volumen de la sustancia que recibe el empuje(_m³)              

Las unidades resultantes son N.

El empuje es una fuerza y todas las fuerzas son medidas en Newtons

Ejemplos

Una bola de acero de 5 cm de radio se sumerge en agua, calcula el empuje que sufre y la fuerza resultante. Datos: Densidad del acero 7,9 g/cm³

El empuje viene dado por E = d_agua · V_sumergido · g   la densidad del agua se da por conocida (1000 kg/m³), nos queda calcular el volumen sumergido, en este caso es el de la bola. Utilizando el volumen de una esfera:           V = 4/3 p R³ = 4/3 p 0,05³ = 5,236 · 10^-4 m³    por tanto el empuje quedará:

E = d_agua·V_sumergido·g  = 1000 · 5,236 · 10^-4 · 9,8 = 5,131 N

Sobre la bola actúa el empuje hacia arriba y su propio peso hacia abajo, la fuerza resultante será la resta de ambas. El empuje ya lo tenemos, calculamos ahora el peso P = m · g, nos hace falta previamente la masa de la bola, ésta se calcula con su densidad y el volumen (la densidad del acero debe estar en S.I.).

d_acero = 7,9 g/cm³ = 7900 kg/m³         m = d_acero · V = 7900 · 5,234 · 10^-4 = 4,135 kg

P = m · g = 4,135 · 9,8 = 40,52 N

Como vemos el peso es mucho mayor que el empuje, la fuerza resultante será P - E = 35,39 N hacia abajo y la bola se irá al fondo.

Un cubo de madera de 10 cm de arista se sumerge en agua, calcula la fuerza resultante sobre el bloque y el porcentaje que permanecerá emergido una vez esté a flote. Datos: densidad de la madera 700 kg/m³

Este ejercicio es muy similar al anterior, el cuerpo es ahora un cubo de volumen V = lado³ = 0,1³ = 0,001 m³ por tanto el empuje será:

E = d_agua·V_sumergido·g  = 1000 · 0,001 · 9,8 = 9,8 N

La masa del bloque será:

m = d_madera · V = 700 · 0,001 = 0,7 kg

y su peso:

P = m · g = 0,7 · 9,8 = 6,86 N

Vemos que el empuje es mayor que el peso, la fuerza resultante es de 2,94 N hacia arriba lo que hace que el cuerpo suba a flote.

Una vez a flote parte del cuerpo emergerá y no el volumen sumergido disminuirá, con lo cual también lo hace el empuje. El bloque quedará en equilibrio a flote cuando el empuje sea igual al peso y no actúe resultante sobre él, calculemos cuánto volumen permanece sumergido cuando esté a flote.

A flote  E = P            d_agua·V_sumergido·g = Peso      1000 · V_sumergido · 9,8 = 6,86

Despejando V_sumergido =  7 · 10^-4 m³ la diferencia de este volumen bajo el agua y el volumen total del bloque será la parte emergida   V_emergido = 0,001 - 7 · 10^-4 = 3 · 10^-4 m³ emergidos.

El porcentaje de bloque emergido será   3 · 10^-4 /0,001 · 100 = 30 %

Se desea calcular la densidad de una pieza metálica, para ello se pesa en el aire dando un peso de 19 N y a continuación se pesa sumergida en agua dando un peso aparente de 17 N. calcula la densidad del metal.

Si en el agua pesa 2 N menos que fuera es que el empuje vale 2 N, utilizando la fórmula del empuje podemos sacar el volumen sumergido, es decir, el volumen de la pieza.

E = d_agua·V_sumergido·g            2 = 1000 · V · 9,8            V = 2,041 · 10^-4 m³

Sabiendo el peso real de la pieza sacamos su masa   m = P/g = 19/9,8 = 1,939 kg.

Ya sabemos el volumen de la pieza y su masa, por tanto su densidad será:

d = m/V = 1,939/2,041 · 10^-4 = 9499 kg/m³

Ejercicios

1. Un objeto de 5 kg se mete en el agua y se hunde siendo su peso aparente en ella de 30 N, calcula el empuje, su volumen y su densidad.

2. Una pieza de 50 g y un volumen de 25 mL, pesa sumergida en un líquido 0,2 N, calcula la densidad del líquido.

3. Calcula el volumen que se encuentra sumergido en un barco de 10000 toneladas si la densidad del agua del mar es 1030 kg/m³

Soluciones:

1.  19 N; 1,939 · 10^-3 m³; 2579 kg/m³

2.  1183 kg/m³

3.  9709 m³

LA DENSIDAD DE LOS CUERPOS

LA DENSIDAD DE LOS CUERPOS

Densidad

Los cuerpos difieren por lo general en su masa y en su volumen. Estos dos atributos físicos varían de un cuerpo a otro, de modo que si consideramos cuerpos de la misma naturaleza, cuanto mayor es el volumen, mayor es la masa del cuerpo considerado.

A diferencia de la masa o el volumen, que dependen de cada objeto, su cociente depende solamente del tipo de material de que está constituido y no de la forma ni del tamaño de aquél.

Densidad y Peso Específico

La densidad está relacionada con el grado de acumulación de materia (un cuerpo compacto es, por lo general, más denso que otro más disperso), pero también lo está con el peso. Así, un cuerpo pequeño que es mucho más pesado que otro más grande es también mucho más denso.
d = densidad
d = m/v = masa/ volumen = kg/m3

Esto es debido a la relación de Peso, asi,

P = m · g existente entre masa y peso.

No obstante, para referirse al peso por unidad de volumen la física ha introducido el concepto de peso específico Pe que se define como el cociente entre el peso P de un cuerpo y su volumen.

El peso específico representa la fuerza con que la Tierra atrae a un volumen unidad de la misma sustancia considerada.
Pe = P/v = peso/volumen = Newton/m3
La unidad del peso específico en el SI es el N/m3

La relación entre peso específico y densidad es la misma que la existente entre peso y masa. En efecto:
siendo g la aceleración de la gravedad.
Peso = P = m*g = masa*gravedad

Sustituimos P en la formula de Pe y tenemos que:
Pe = (m*g)/v = d*g = densidad por aceleración de la gravedad

Densidades de algunos elementos

Agua = 1000 kg/m3
Glicerina = 1260
Alcohol etílico = 810
Madera de pino = 420
Platino = 21400
Huesos = 1700 y 2000

EJERCICIOS

Resolver los siguientes ejercicios propuestos en grupo de 4 estudiantes y traerlos como trabajo en hojas para la próxima clase después de Semana Santa.

b) ¿Es posible que el objeto X el objeto W sean de la misma sustancia? Sí o no y por qué. 

1.- Para determinar la densidad de un trozo de oro, se midió su masa y se encontró un valor igual que 50g; al medir su volumen éste fue de 2.587 cm³. Calcular la densidad.

2.- Para cuantificar la densidad del agua en el laboratorio se midieron 10 cm³ de agua y se determinó su masa con la balanza, encontrándose un valor de 10g.

Calcular:

a) ¿Cuánto vale la densidad del agua?

b) Si en lugar de 10 cm³ midiéramos 1000 cm³, ¿cambiaría el valor de la densidad del agua?

c) ¿Qué volumen ocuparán 600g de agua?

3.- 0.5 kg de alcohol etílico ocupan un volumen de 0.000633 cm³.

Calcular:

a) ¿Cuál es su densidad?

b) ¿Cuál es su peso específico?

4.- Calcular la masa y el peso de 15 000 litros de gasolina. Densidad de la gasolina 700 kg/m³.

5.- ¿Cuál es la densidad de un aceite cuyo peso específico es de 8 967 N/m³?

6.- Si te mostraran dos frascos de vidrio perfectamente tapados, con una capacidad de un litro cada uno, llenos de un líquido incoloro y te preguntaran si son de la misma sustancia, ¿cómo harías para responder sin necesidad de destapar los frascos?

7.- Si para hallar la densidad del cobre te dan a escoger entre un cubo de 1 cm³de volumen y una barra de 10 kg de masa, ¿con cuál de los dos determinarías la densidad?

8.- Determinar el volumen de un trozo de corcho si su densidad es de

0.23 g/cm³ y tiene una masa de 50 g. Además, decir si flota o no corcho al sumergirlo en un recipiente lleno de agua; justifica tu respuesta.

9.- Un cubo de aluminio presenta 2 cm de longitud en uno de sus lados y tiene una masa de 21.2 g.

Calcular:

a) ¿Cuál es su densidad?

b) ¿Cuál será la masa de 5.5 cm³ de aluminio?

10.- ¿Cuál es el volumen, en metros cúbicos y el litros, de 3 000 N de aceite de oliva, cuyo peso específico es de 9 016 N/m³?

11.- Un objeto Y tiene una masa de 150g y una densidad de 2 g/cm³, un objeto Z tiene una masa de 750g y una densidad de 10 g/cm³.

a) Si se introducen por separado los dos objetos en un recipiente con agua, determinar cuál desplazará mayor volumen de agua.

Presión hidrostática, Prensa hidráulica y principio de Pascal

La presión hidrostática, es la que se manifiesta en el interior de toda masa líquida, provocada por el peso de una columna de líquido que debe soportar un cuerpo sumergido.

Un fluido pesa y ejerce presión sobre las paredes y el fondo del recipiente que lo contiene. Esta presión, llamada presión hidrostática, provoca, en fluidos en reposo, una fuerza perpendicular a las paredes del recipiente ,sin importar la orientación que adopten las caras. 

Algunas caracteristicas son:

1-La presión del interior de un líquido actúa en todas las direcciones

2-la presión es más alta cuanto mayor sea la profundidad

3-La presión es mayor cuanto mayor sea la densidad del líquido.

4-La presión no depende de la forma ni de la amplitud del recipiente.

La presión hidrostática se calcula con la fórmula:

Ph= Pe h  o bien  Ph= P g h

Ph= presión Hidrostática en N/metros cuadrados

P= Densidad del líquido en Kg/metros cúbicos

Pe= peso específico del liquido en N/metros cúbicos

g= valor de la aceleración de la gravedad

H= altura de la superficie libre en metros

PRENSA HIDRÁULICA

La prensa hidráulica es una máquina capaz de generar una fuerza elevada aplicando sobre ella una fuerza relativamente pequeña.

Se componen dos aberturas, una de superficie mayor (A₂) y otra de menor (A₁). Dicho depósito se rellena con un fluido, en cada abertura se sitúa un émbolo..

Si se aplica una fuerza sobre el émbolo pequeño, introduciéndolo en el recipiente, la presión se transmite íntegramente a todo el líquido, haciendo que el émbolo grande ascienda con una fuerza mayor que la aplicada en el émbolo pequeño.

PRINCIPIO DE PASCAL

En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: la presión ejercida en cualquier lugar de un fluido encerrado e incompresible se transmite por igual en todas las direcciones en todo el fluido, es decir, la presión en todo el fluido es constante.

La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.

EJEMPLOS

1) Se desea elevar un cuerpo de 1500kg utilizando una elevadora hidráulica de plato grande
circular de 90cm de radio y plato pequeño circular de 10cm de radio. Calcula cuánta fuerza hay
que hacer en el émbolo pequeño para elevar el cuerpo.
Recordemos en primer lugar la fórmula del Principio de Pascal, que nos permitirá resolver todos
estos problemas relativos a prensas hidráulicas:
F1/S1 = F2/S2
Las dos F son, obviamente, las fuerzas ejercidas sobre los dos émbolos o platos, cada uno con una
superficie S. La idea es que, en una prensa hidráulica, una fuerza pequeña sobre el plato pequeño
nos sirve para mover un peso (fuerza) grande sobre el plato grande.
Calculamos cada uno de los términos:
F1 = ?
F2 = P2 = m2·g = 1500·9,8 = 14700N
S1 = π·R1
2
 = π·0,12
 = 0,0314m2
S2 = π·R2
2
 = π·0,92
 = 2,54m2
F1/S1 = F2/S2
F1/0,0314 = 14700/2,54
F1 = 5787,40·0,0314 = 181,72N
Obviamente, nos tiene que salir una fuerza mucho más pequeña que F2 (el peso sobre el émbolo
grande).
www.cajondeciencias.com
Cajón de Ciencias
2) Calcula la fuerza obtenida en el émbolo mayor de una prensa hidráulica si en el menor se hacen
15N y los émbolos circulares tienen cuádruple radio uno del otro.
Muy parecido al anterior, y si parece que faltan datos es porque no nos hacen falta. Vamos a
sustituir lo que sabemos en la fórmula del principio de Pascal:
F1 = 15N
F2 = ?
S1 = π·R1
2
(no podemos sustituir nada, así que lo dejamos así)
S2 = π·R2
2
 = π·(4R1)
2
 = π· 16R1
2
F1/S1 = F2/S2
15/π·R1
2 = F2/π·16R1
2
Simplificamos
15/1 = F2/16
F2 = 15·16 = 240N
3) Sobre el plato menor de una prensa se coloca una masa de 16kg. Calcula qué masa se podría
levantar colocada en el plato mayor, cuyo radio es el doble del radio del plato menor.
Casi idéntico al anterior, solo que en lugar de fuerzas nos hablan de masa. Sin embargo, eso no
supone ningún problema: ya que en ambos platos la fuerza es igual al peso, que es igual a la masa
por la aceleración de la gravedad, el término g se simplifica en ambos lados (mientras ambos platos
de la presa estén en el mismo planeta, claro está). Moraleja: en el principio de Pascal podemos
trabajar con masas igual que trabajamos con pesos o fuerzas.
F1/S1 = F2/S2
m1·g/S1 = m2·g/S2
m1/S1 = m2/S2
16/π·R1
2 = m2/π·4R1
2
16/1 = m2/4
m2 = 16·4 = 64 Kg
www.cajondeciencias.com
Cajón de Ciencias
4) ¿Qué proporción deberían guardar los platos de una prensa hidráulica para que, aplicando 40N
de fuerza en el plato menor, podamos levantar un objeto de 80Kg en el plato mayor?
Una mezcla de los anteriores. Parece que falta algún dato, pero que no cunda el pánico. Vamos a
colocar primero todo lo que sabemos:
F1 = 40N
F2 = 80·9,8 = 784N
S1 = ?
S2 = ?
¿Hay dos incógnitas? No. Fíjate que lo que nos preguntan no es cuánto vale cada superficie, sino
qué proporción hay entre ellas, es decir, si una es el doble, el triple, etc. que la otra.
40/S1 = 784/S2
40·S2 = 784·S1
S2/S1 = 784/40
S2/S1 = 19,6
O lo que es lo mismo, la supeficie del émbolo grande debe ser 19,6 veces la del émbolo pequeño
para poder hacer lo que nos dice el enunciado.
(Un último detalle: este resultado va sin unidades, porque es una proporción. ¡No te confundas!)
5) Una cuestión teórica: ¿qué partes del interior de una prensa hidráulica se ven sometidas a una
mayor presión mientras aplicamos la fuerza en los émbolos?
Recordemos el dibujo esquema de una prensa hidráulica:
Las respuestas más habituales a la pregunta del enunciado son “la zona que está justo debajo del
émbolo pequeño”, “la zona de los émbolos” o “las paredes del tubo del émbolo pequeño”. Todas
son falsas, y demuestran que, aunque los que las dicen sepan resolver problemas usando la fórmula
del principio de Pascal, se han olvidado de cuál es el fénomeno físico que es la base de este
principio:
“La presión sobre las paredes de un recipiente que contiene un líquido
se reparte siempre de manera uniforme.”
Es decir, la formulita con las fuerzas y las superficies es así por la sencilla razón de que la presión

sobre ambos émbolos es igual, y lo mismo se aplica a todas las paredes de la prensa hidráulica.

Hidrostática, Propiedades de fluidos y Presión

La hidrostática, por su parte, es la rama de la mecánica que se especializa en el equilibrio de los fluidos. El término también se utiliza como adjetivo para referirse a lo que pertenece o está vinculado a dicha área de la mecánica.




PROPIEDADES DE FLUIDOS

Las propiedades de un fluido son las que definen el comportamiento y características del mismo tanto en reposo como en movimiento. Existen propiedades primarias y propiedades secundarias del fluido.

Propiedades primarias o termodinámicas

Densidad

Presión

Temperatura

Energía interna

Entalpía

Entropía

Calores específicos

Propiedades Secundarias

Caracterizan el comportamiento específico de los fluidos.

Viscosidad

Conductividad térmica

Tensión superficial

Compresión

PRESIÓN

La presión es una magnitud física que mide la proyección de la fuerza en dirección perpendicular por unidad de superficie, y sirve para caracterizar cómo se aplica una determinada fuerza resultante sobre una línea.

Para calcular la presión utilizamos la formula:

P= N/A

N= Fuerza 

A= Área

P= Presión

Ejemplos

Calcula la presión a una profundidad de 20 metros en el mar sabiendo que la densidad del agua del mar es de 1,03 kg/L.
Aplicamos la expresión  p = d · g · h, antes de nada debemos pasar la densidad del agua de mar a kg/m³, para
 ello utilizamos factores de conversión:
Por tanto:   p = d · g · h = 1030 · 9,8 · 20 = 201880 Pa

Calcula la fuerza que actúa sobre una chapa cuadrada de 10 cm de lado sumergida en agua a una profundidad de 40 cm. Densidad del agua 1000 kg/m³.
Calculamos la presión a esa profundidad: p = d · g · h = 1000 · 9,8 · 0,4 = 3920 Pa
y ahora despejamos la fuerza de la ecuación de definición de la presión:                   Þ 


Debemos calcular la superficie de la chapa que como es un cuadrado será  0,1 · 0,1 = 0,01 m²
Y ya podemos calcular la fuerza sobre la chapa  F = p · S = 3920 · 0,01 = 39,2 N

Ejercicios
1. ¿Qué fuerza actúa sobre la espalda de un buceador si bucea a 3 m de profundidad en agua dulce y su espalda tiene una superficie de 0,3 m²?
2. Un submarino puede bajar hasta los 2000 m de profundidad en agua dulce, calcula la presión que soporta. ¿A qué profundidad podría bajar si se sumerge en mercurio que tiene una densidad de 13600 g/L?
3. ¿Con qué fuerza hay que tirar para quitar el tapón de una bañera llena de agua hasta los 80 cm si el tapón es circular y de radio 3 cm?







Soluciones:
1.   8820 N
2.   19,6 · 10⁷ Pa; 147 m

3.   22,17 N

Estados de agregación y Elasticidad

¿QUE SON LO ESTADOS DE AGREGACIÓN?

En física y química se observa que, para cualquier sustancia o mezcla, modificando sus condiciones de temperatura o presión, pueden obtenerse distintos estados o fases, denominados estados de agregación de la materia, en relación con las fuerzas de unión de las partículas (moléculas, átomos o iones) que la constituyen.

La materia se presenta en cuatro estados o formas de agregación: sólido, líquido, gaseoso y plasma.

SÓLIDOS:

 Tienen forma y volumen constantes. Se caracterizan por la rigidez y regularidad de sus estructuras. Los sólidos se caracterizan por tener forma y volumen constantes. Esto se debe a que las partículas que los forman están unidas por unas fuerzas de atracción grandes de modo que ocupan posiciones casi fijas.

LÍQUIDOS:

 Los líquidos tienen volumen constante. En los líquidos las partículas están unidas por unas fuerzas de atracción menores que en los sólidos, por esta razón las partículas de un líquido pueden trasladarse con libertad. 



GASEOSO:

 Estado de agregación de la materia compuesto principalmente por moléculas no unidas, expandidas y con poca fuerza de atracción, lo que hace que los gases no tengan volumen y forma definida, y se expandan libremente hasta llenar el recipiente que los contiene.

PLASMA:

Cuarto estado de agregación de la materia, un estado fluido similar al estado gaseoso pero en el que determinada proporción de sus partículas están cargadas eléctricamente y no poseen equilibrio electromagnético, por eso son buenos conductores eléctricos y sus partículas responden fuertemente a las interacciones electromagnéticas de largo alcance.

ELASTICIDAD

En física el término elasticidad designa la propiedad mecánica de ciertos materiales de sufrir deformaciones reversibles cuando se encuentran sujetos a la acción de fuerzas exteriores y de recuperar la forma original si estas fuerzas exteriores se eliminan.

Esfuerzo y deformación, tensión y comprensión unitarias.

Ley de Hoo

Modulo de Elasticidad

Modulo de Young

Limite elástico

Existen tres tipos de tensión

 Esfuerzo de tensión: Se presenta cuando sobre un cuerpo actúan fuerzas de igual magnitud, pero de sentido contrario que se alejan entre si.

Esfuerzo de compresión: Ocurre cuando sobre un cuerpo actúan fuerzas iguales en magnitud, pero de sentido contrario que se acercan entre si.

Esfuerzo de Corte: Se presenta cuando sobre un cuerpo actúan fuerzas colineales de igual o diferente magnitud que se mueven en sentidos contrarios.

para la elasticidad-esfuerzo y deformación se aplica la formula:

E= esfuerzo

F= fuerza

A= área donde se aplica la fuerza

E= F/A