Segunda condición de equilibrio

-Segunda condición de equilibrio: 

Por otro lado, diremos que un cuerpo está en equilibrio de rotación cuando la suma de todas las fuerzas que se ejercen en él respecto a cualquier punto es nula. O dicho de otro modo, cuando la suma de los momentos de torsión es cero.

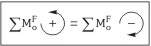
En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):

Un cuerpo se encuentra en equilibrio traslacional y rotacional cuando se verifiquen de forma simultánea las dos condiciones de equilibrio. Estas condiciones de equilibrio se convierten, gracias al álgebra vectorial, en un sistema de ecuaciones cuya solución será la solución de la condición del equilibrio.

SEGUNDA CONDICIÓN DEL EQUILIBRIO
Para que un cuerpo esté en equilibrio derotación, debe cumplirse la segunda condición que
dice: para que un cuerpo esté en equilibrio de rotación, la suma de los momentos o torques de
fuerzas que actúan sobre él respecto a cualquier punto debe ser igual a cero. Es decir:
= 0
EJEMPLO 1
Encontrar la magnitud de una tercera fuerza F3, que aplicada a dos metros del eje de giro del
aspa que se muestra en la siguiente figura se encuentre en equilibrio rotacional.
Solución
Aplicamos la segunda condición del equilibrio y sumamos todos los momentos en el eje de
rotación:
∑Mo = 0
- F1
 (5m) – F2
 (5m) + F3
 (2m) =0
F3
 (2m) = (10 N) (5m) + (10 N) (5m)
=
100
2
F3
 = 50 N
F1 = 10 N
F2 = 10 N
F3
5 m 5 m
2 m 
EJEMPLO 2
Una barra sin peso se mantiene en equilibrio, tal como se muestra en la figura. Hallar el valor
del peso w
Solución:
En el diagrama de cuerpo libre se puede apreciar la fuerza R que es la fuerza de reacción que
ejerce el soporte sobre la barra. Aplicando la segunda condición del equilibrio sobre el punto R
tenemos que:
∑MR
 = 0
(20 N) (3 m) – (w) (2 m) = 0
Despejando w nos queda
=
20 3
2

W = 30 N