Primera condición de equilibrio.

PRIMERA CONDICIÓN DEL EQUILIBRIO.

-Primera condición de equilibrio: Diremos que un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante de todas las fuerzas que actúan sobre él es nula: ∑ F = 0.
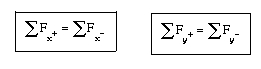
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:

Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.

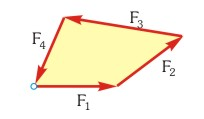
El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).

Consideremos un objeto que cuelga de una cuerda, como se muestra en la figura. Sobre el
objeto actúan dos fuerzas: una de ellas es la tensión de la cuerda que impide que el objeto
caiga, la otra es la fuerza de gravedad, la cual actúa sobre el objeto atrayéndolo hacia abajo, a
dicha fuerza la definimos como el peso del objeto.
En resumen tenemos que:
 = 0
REGLAS PARA RESOLVER PROBLEMAS APLICANDO LA PRIMERA CONDICIÓN
DEL EQUILIBRIO:
1. Considere todas las fuerzas que actúan sobre el cuerpo en cuestión.
2. Traza un diagrama de cuerpo libre y establece un sistema de coordenadas cartesianas.
3. Lleva a cabo la descomposición de las fuerzas sobre los ejes X y Y.
4. Iguala a cero la suma algebraica de las componentes escalares sobre cada eje (primera
condición del equilibrio).
5. Resuelve el sistema de ecuaciones resultante
T
W
EJEMPLO1:
Un bloque de 20 N se suspende por medio de una cuerda sin peso, que se mantiene formando
un ángulo de 60º con la vertical, mediante una cuerda horizontal. Hallar la magnitud de las
tensiones T1 y T2
Solución:
Aplicando las reglas 3 y 4 obtenemos lo siguiente:
= 0
T2
 – T1x = 0
T2
 – T1
 Cos 30=0
T2
 = T1
 Cos 30 ------------------------------> (1)
= 0
T1y – W = 0
T1
 Sen 30 – W =0
T1
 Sen 30 = 20N
T1
 =



=

.
T1= 40N
Sustituyendo T1
 en la ecuación (1) tenemos que:
T2
 = 40N Cos 30 = (40) (0.87)
T2
 = 34.8 N