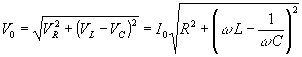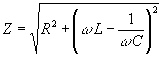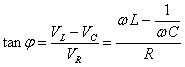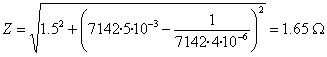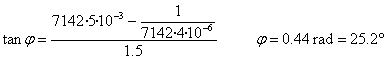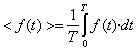LA CORRIENTE ALTERNA (C.A.)

Además de la existencia de fuentes de FEM de corriente directa o continua (C.D.) (como la que suministran las pilas o las baterías, cuya tensión o voltaje mantiene siempre su polaridad fija), se genera también otro tipo de corriente denominada alterna (C.A.), que se diferencia de la directa por el cambio constante de polaridad que efectúa por cada ciclo de tiempo.

Una pila o batería constituye una fuente de suministro de corriente directa, porque su polaridad se mantiene siempre fija. La característica principal de una corriente alterna es que durante un instante de tiempo un polo es negativo y el otro positivo, mientras que en el instante siguiente las polaridades se invierten tantas veces como ciclos por segundo o hertz posea esa corriente. No obstante, aunque se produzca un constante cambio de polaridad, la corriente siempre fluirá del polo negativo al positivo, tal como ocurre en las fuentes de FEM que suministran corriente directa. Veamos un ejemplo práctico que ayudará a comprender mejor el concepto de corriente alterna:

Corriente alterna pulsante de un ciclo por segundo o hertz (Hz) . Si hacemos que la pila del ejemplo anterior gire a una determinada velocidad, se producirá un cambio constante de polaridad en los bornes donde hacen contacto los dos polos de dicha pila. Esta acción hará que se genere una corriente alterna tipo pulsante, cuya frecuencia dependerá de la cantidad de veces que se haga girar la manivela a la que está sujeta la pila para completar una o varias vueltas completas durante un segundo. En este caso si hacemos una representación gráfica utilizando un eje de coordenadas para la tensión o voltaje y otro eje para el tiempo en segundos, se obtendrá una corriente alterna de forma rectangular o pulsante, que parte primero de cero volt, se eleva a 1,5 volt, pasa por “0” volt, desciende para volver a 1,5 volt y comienza a subir de nuevo para completar un ciclo al pasar otra vez por cero volt. Si la velocidad a la que hacemos girar la pila es de una vuelta completa cada segundo, la frecuencia de la corriente alterna que se obtiene será de un ciclo por segundo o hertz (1 Hz). Si aumentamos ahora la velocidad de giro a 5 vueltas por segundo, la frecuencia será de 5 ciclos por segundo o hertz (5 Hz). Mientras más rápido hagamos girar la manivela a la que está sujeta la pila, mayor será la frecuencia de la corriente alterna pulsante que se obtiene. Seguramente sabrás que la corriente eléctrica que llega a nuestras casas para hacer funcionar las luces, los equipos electrodomésticos, electrónicos, etc. es, precisamente, alterna, pero en lugar de pulsante es del tipo sinusoidal o senoidal. En Europa la corriente alterna que llega a los hogares es de 220 volt y tiene una frecuencia de 50 Hz, mientras que en la mayoría de los países de América la tensión de la corriente es de 110 ó 120 volt, con una frecuencia de 60 Hz. La forma más común de generar corriente alterna es empleando grandes generadores o alternadores ubicados en plantas termoeléctricas, hidroeléctricas o centrales atómicas. FORMAS DIFERENTES QUE TOMA LA CORRIENTE ALTERNA De acuerdo con su forma gráfica, la corriente alterna puede ser: Rectangular o pulsante Triangular Diente de sierra Sinusoidal o senoidal (A) Onda rectangular o pulsante. (B) Onda triangular. (C) Onda diente de sierra. (D) Onda sinusoidal o senoidal. De todas estas formas, la onda más común es la sinusoidal o senoidal. Cualquier corriente alterna puede fluir a través de diferentes dispositivos eléctricos, como pueden ser resistencias, bobinas, condensadores, etc., sin sufrir deformación. La onda con la que se representa gráficamente la corriente sinusoidal recibe ese nombre porque su forma se obtiene a partir de la función matemática de seno. En la siguiente figura se puede ver la representación gráfica de una onda sinusoidal y las diferentes partes que la componen: De donde: A = Amplitud de onda P = Pico o cresta N = Nodo o valor cero V = Valle o vientre T = Período Amplitud de onda: máximo valor que toma una corriente eléctrica. Se llama también valor de pico o valor de cresta. Pico o cresta: punto donde la sinusoide alcanza su máximo valor. Nodo o cero: punto donde la sinusoide toma valor “0”. Valle o vientre: punto donde la sinusoide alcanza su mínimo valor. Período: tiempo en segundos durante el cual se repite el valor de la corriente. Es el intervalo que separa dos puntos sucesivos de un mismo valor en la sinusoide. El período es lo inverso de la frecuencia y, matemáticamente, se representa por medio de la siguiente fórmula:     T = 1 / F Como ya se vio anteriormente, la frecuencia no es más que la cantidad de ciclos por segundo o hertz (Hz), que alcanza la corriente alterna. Es el inverso del período y, matemáticamente, se representa de la manera siguiente:   F = 1 / T CIRCUITOS RL             Los circuitos RL son aquellos que contienen una bobina (inductor) que tiene autoinductancia, esto quiere decir que evita cambios instantáneos en la corriente. Siempre se desprecia la autoinductancia en el resto del circuito puesto que se considera mucho menor a la del inductor. Para un tiempo igual a cero, la corriente comenzará a crecer y el inductor producirá igualmente una fuerza electromotriz en sentido contrario, lo cual hará que la corriente no aumente. A esto se le conoce como fuerza contraelectromotriz. Esta fem está dada por:  V = -L (inductancia) dI/dt Debido a que la corriente aumentará con el tiempo, el cambio será positivo (dI/dt) y la tensión será negativa al haber una caída de la misma en el inductor. Según kirchhoff:                     V = (IR) + [L (dI /  dt)]          IR = Caída de voltaje a través de la resistencia. Esta es una ecuación diferencial y se puede hacer la sustitución:                x = (V/R) – I           es decir;       dx = -dI Sustituyendo en la ecuación:     x + [(L/R)(dx/dt)] = 0      dx/x = - (R/L) dt Integrando:                                  ln (x/xo) = -(R/L) t Despejando x:                               x = xo e –Rt / L Debido a que                                     xo = V/R El tiempo es cero , y corriente cero              V/R – I = V/R e –Rt / L                                  I = (V/R) (1 - e –Rt / L) El tiempo  del circuito está representado por  t = L/R                                  I = (V/R) (1 – e – 1/t)  Donde para un tiempo infinito, la corriente de la malla será  I = V/R. Y se puede considerar entonces el cambio de la corriente en el tiempo como cero. Para verificar la ecuación que implica a t y a I, se deriva una vez y se reemplaza en la inicial:                                  dI/dt = V/L e – 1/t  Se sustituye:                             V = (IR) + [L (dI /  dt)]  V = [ (V/R) (1 – e – 1/t)R + (L V/ L e – 1/t)]  V – V e – 1/t = V – V e – 1/t    OSCILACIONES EN UN CIRCUITO LC Cuando un condensador se conecta a un inductor, tanto la corriente como la carga den el condensador oscila. Cuando existe una resistencia, hay una disipación de energía en el sistema porque una cuanta se convierte en calor en la resistencia, por lo tanto las oscilaciones son amortiguadas. Por el momento, se ignorará la resistencia. En un tiempo igual a cero, la carga en el condensador es máxima y la energía almacenada en el campo eléctrico entre las placas es U = Q2máx/(2C). Después de un tiempo igual a cero, la corriente en el circuito comienza a aumentar y parte de la energía en el condensador se transfiere al inductor. Cuando la carga almacenada en el condensador es cero, la corriente es máxima y toda la energía está almacenada en el campo eléctrico del inductor. Este proceso se repite de forma inversa y así comienza a oscilar. En un tiempo determinado, la energía total del sistema es igual a la suma de las dos energías (inductor y condensador):  U = Uc + UL  U = [ Q2/(2C) ] + ( LI2/2 ) CIRCUITOS RC    Los circuitos RC son circuitos que están compuestos por una resistencia y un condensador.   Se caracteriza por que la corriente puede variar con el tiempo. Cuando el tiempo es igual a cero, el condensador está descargado, en el momento que empieza a correr el tiempo, el condensador comienza a cargarse ya que hay una corriente en el circuito. Debido al espacio entre las placas del condensador, en el circuito no circula corriente, es por eso que se utiliza una resistencia. Cuando el condensador se carga completamente, la corriente en el circuito es igual a cero. La segunda regla de Kirchoff dice:  V = (IR) – (q/C) Donde q/C es la diferencia de potencial en el condensador. En un tiempo igual a cero, la corriente será:  I = V/R  cuando el condensador no se ha cargado. Cuando el condensador se ha cargado completamente, la corriente es cero y la carga será igual a: Q = CV CARGA DE UN CONDENSADOR Ya se conoce que las variables dependiendo del tiempo serán I y q. Y la corriente I se sustituye por dq/dt (variación de la carga dependiendo de la variación del  tiempo): (dq/dt)R = V – (q/C)  dq/dt = V/R – (q/(RC)) Esta es una ecuación Diferencial. Se pueden             dq/dt = (VC – q)/(RC) Separar variable                      dq/(q – VC) = - dt/(RC) Al integrar se tiene              ln [ - (q – VC)/VC)] = -t/(RC Despejando q                  q dt = C V [(1 – e-t/RC )] = q (1- e-t/RC  )   El voltaje será                            ) = V        DESCARGA DE UN CONDENSADOR Debido a que la diferencia de potencial en el condensador es IR = q/C, la razón de cambio de carga en el condensador determinará la corriente en el circuito, por lo tanto, la ecuación que resulte de la relación entre el cambio de la cantidad de carga dependiendo del cambio en el tiempo y la corriente en el circuito, estará dada remplazando I = dq/dt en la ecuación de diferencia de potencial en el condensador: q = Q e-t/RC Donde Q es la carga máxima La corriente en función del tiempo entonces, resultará al derivar esta ecuación respecto al tiempo: I = Q/(RC) e-t/RC Se puede concluir entonces, que la corriente y la carga decaen de forma exponencial. 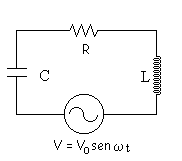Circuito LCR en serie Dibujamos el diagrama de vectores teniendo en cuenta: que la intensidad que pasa por todos los elementos es la misma, que la suma (vectorial) de las diferencias de potencial entre los extremos de los tres elementos nos da la diferencia de potencial en el generador de corriente alterna. 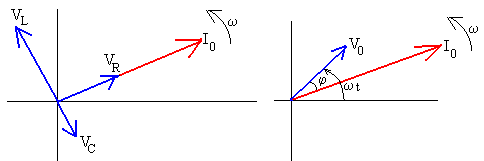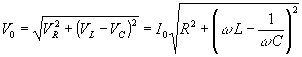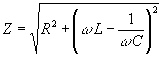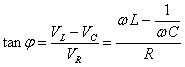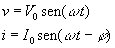El vector resultante de la suma de los tres vectores es Se denomina impedancia del circuito al término de modo que se cumpla una relación análoga a la de los circuitos de corriente continua V0=I0·Z.El ángulo que forma el vector resultante de longitud V0 con el vector que representa la intensidad I0 es Las expresiones de la fem y de la intensidad del circuito son La intensidad de la corriente en el circuito está atrasada un ángulo j respecto de la fem que suministra el generador. 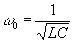Actividades En el applet se introducen los siguientes datos: Resistencia en W Capacidad en microfaradios (10-6 F) Autoinducción en mH (10-3 H) El cociente w/w0 entre la frecuencia w del generador y la frecuencia propia del circuito w0 Se pulsa el botón titulado Empieza. Se observa los valores instantáneos de la corriente i en el circuito LCR y de la diferencia de potencial (ddp) V del generador a medida que transcurre el tiempo. A la izquierda, como proyecciones sobre el eje vertical de los vectores rotatorios que representan a la intensidad y la ddp. A la derecha, la representación gráfica de los valores de la intensidad y de la ddp en función del tiempo. Observar las relaciones de fase entre la intensidad y la ddp en el generador en los siguientes casos w =w0 w >w0 w <w0 Ejemplo: R=1.5 Ω L=5·10-3 H C=4·10-6 F ω=1.01·w0 La frecuencia propia del circuito es La frecuencia del generador es ω=1.01·w0=7142 rad/s La impedancia vale El desfase es FemApplet aparecerá en un explorador compatible JDK 1.1   Resonancia en un circuito LCR en serie La condición de resonancia la estudiamos en las oscilaciones forzadas de una masa unida a un muelle elástico. La potencia suministrada por el generador de corriente alterna es P=i·v=V0·I0sen(w t)·sen(w t-j ) P=V0·I0sen(w t)·(sen(w t)·cos j - cos(w t)·senj)=V0·I0(sen2(w t)·cos j - sen(w t)·cos(w t)·senj) Esta magnitud es una función complicada del tiempo que no es útil desde el punto de vista práctico. Lo que tiene interés es el promedio de la potencia en un periodo 2p /w . 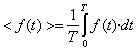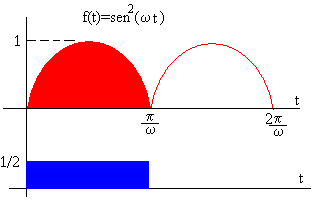<P>=V0·I0(<sen2(w t)>·cos j - <sen(w t)·cos(w t)>·senj) Se define como valor medio <f(t)> de una función periódica f(t) de periodo T a la integral El periodo de la función f(t)=sen2(w t) es T=π/ω, su valor medio es <sen2(w t)>=1/2 El área de color rojo es igual al área de color azul. 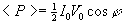El periodo de la función f(t)=sen(w t)·cos(w t)=sen(2w t)/2 es T=π/ω, su valor medio es <sen(w t)·cos(w t)>=0 como puede comprobarse fácilmente El valor medio de la energía por unidad de tiempo, o potencia suministrada por el generador es El último término, cosj se denomina factor de potencia. 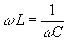El valor de <P> es máximo cuando el ángulo de desfase j es cero, para ello se tiene que cumplir que es decir, la frecuencia w del generador de corriente alterna debe coincidir con la frecuencia natural o propia w0 del circuito oscilante. Cuando w =w0 se cumple que La intensidad de la corriente I0 alcanza su valor máximo La intensidad de la corriente en el circuito i y la fem v están en fase La energía por unidad de tiempo <P> suministrada por el generador es máxima Actividades En el applet se introducen los siguientes datos: Resistencia en W Capacidad en mF (10-6 F) Autoinducción en mH (10-3 H) Se escoge la magnitud que deseamos representar en función del cociente w /w0 Potencia <P> Amplitud de la intensidad I0 Desfase j entre la intensidad y la fem del generador Representación de la potencia <P> En la representación de la potencia <P> observamos que cuando la frecuencia del generador w coincide con la frecuencia de resonancia w0 la potencia alcanza un máximo. Se representa también el intervalo de frecuencias Dw para los cuales la potencia es mayor que la mitad de la máxima. La agudeza de la curva de resonancia se describe mediante un parámetro adimensional denominado factor de calidad Q0 que se define como el cociente entre la frecuencia angular de resonancia w0 y el ancho de la curva de resonancia Dw. 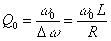Manteniendo fijos los valores de la capacidad del condensador y de la autoinducción de la bobina, se modifica el valor de la resistencia R. ¿Cómo cambia la curva de resonancia?. Representación de la amplitud de la intensidad La amplitud de la intensidad I0 adquiere un valor máximo cuando la frecuencia del generador w coincide con la frecuencia de resonancia w0. El valor de la impedancia Z es mínimo y vale Z=R. Manteniendo fijos los valores de la capacidad del condensador y de la autoinducción de la bobina, se modifica el valor de la resistencia R. ¿Cómo cambia la curva que representa la amplitud en función del cociente w /w0? Representación del desfase entre la intensidad y la fem El desfase entre la intensidad y la fem se hace cero cuando la frecuencia del generador w coincide con la frecuencia de resonancia w0. La intensidad y la fem están en fase a esta frecuencia La diferencia de fase cambia de signo, cuando la frecuencia w es mayor que  la frecuencia de resonancia w0, y aumenta rápidamente cuando nos alejamos de dicha frecuencia, sobre todo si la resistencia es pequeña.

La corriente eléctrica o intensidad eléctrica es el flujo de carga eléctrica por unidad de tiempo que recorre un material. Se debe al movimiento de las cargas (normalmente 
electrones) en el interior del material.

CORRIENTE DIRECTA O CONTINUA

La corriente directa (CD) o corriente continua (CC) es aquella cuyas cargas eléctricas o electrones fluyen siempre en el mismo sentido en un circuito eléctrico cerrado, moviéndose del polo negativo hacia el polo positivo de una fuente de fuerza electromotriz (FEM), tal como ocurre en las baterías, las dinamos o en cualquier otra fuente generadora de ese tipo de corriente eléctrica.

Fuentes suministradoras de corriente directa o continua. A la izquierda, una batería de las comúnmente utilizada en los coches y todo tipo de vehículo motorizado. A la derecha, pilas de amplio uso, lo mismo en linternas que en aparatos y dispositivos eléctricos y electrónicos.

Es importante conocer que ni las baterías, ni los generadores, ni ningún otro dispositivo similar crea cargas eléctricas pues, de hecho, todos los elementos conocidos en la naturaleza las contienen, pero para establecer el flujo en forma de corriente eléctrica es necesario ponerlas en movimiento.

El movimiento de las cargas eléctricas se asemeja al de las moléculas de un líquido, cuando al ser  impulsadas por una bomba circulan a través de la tubería de un circuito hidráulico cerrado.

Las cargas eléctricas se pueden comparar con el líquido contenido en la tubería de una instalación hidráulica. Si la función de una bomba hidráulica es poner en movimiento el líquido contenido en una tubería, la función de la tensión o voltaje que proporciona la fuente de fuerza electromotriz (FEM) es, precisamente, bombear o poner en movimiento las cargas contenidas en el cable conductor del circuito eléctrico. Los elementos o materiales que mejor permiten el flujo de cargas eléctricas son los metales y reciben el nombre de “conductores”.

Como se habrá podido comprender, sin una tensión o voltaje ejerciendo presión sobre las cargas eléctricas no puede haber flujo de corriente eléctrica. Por esa íntima relación que existe entre el voltaje y la corriente generalmente en los gráficos de corriente directa, lo que se representa por medio de los ejes de coordenadas es el valor de la tensión o voltaje que suministra la fuente de FEM.

Circuito eléctrico compuesto por una pila o fuente de suministro de FEM; una bombilla, carga o<.consumidor conectada al circuito  y  los  correspondientes  conductores  o  cables  por  donde  fluye  la.<corriente eléctrica. A la derecha aparece la representación gráfica del suministro de 1,5 volt de la pila< (eje. de coordenadas "y") y el tiempo que permanece  la pila suministrando corriente a la bombilla.<(representado por el eje de coordenadas "x").

La coordenada horizontal “x” representa el tiempo que la corriente se mantiene fluyendo por circuito eléctrico y la coordenada vertical “y” corresponde al valor de la tensión o voltaje que suministra la fuente de fem (en este caso una pila) y se aplica circuito. La representación gráfica del voltaje estará dada entonces por una línea recta horizontal continua, siempre que el valor de la tensión o voltaje se mantenga constante durante todo el tiempo.

Normalmente cuando una pila se encuentra completamente cargada suministra una FEM, tensión o voltaje de 1,5 volt. Si representamos gráficamente el valor de esa tensión o voltaje durante el tiempo que la corriente se mantiene fluyendo por el circuito cerrado, obtenemos una línea recta. Si después hacemos girar la pila invirtiendo su posición y representamos de nuevo el valor de la tensión o voltaje, el resultado sería el mismo, porque en ambos casos la corriente que suministra la fuente de FEM sigue siendo directa o continua. Lo único que ha cambiado es el sentido del flujo de corriente en el circuito, provocado por el cambio de posición de la pila, aunque en ambos casos el sentido de circulación de la corriente seguirá siendo siempre del polo negativo al positivo. Mallas y Nodos Una rama es un solo elemento, ya sea si este es activo o pasivo. En otras palabras, una rama representa a cualquier elemento de dos terminales. Un nodo es un punto de conexión entre dos o más ramas. Comúnmente un nodo es representado con un punto en un circuito. Si un cortocircuito conecta a dos nodos, estos son vistos como un solo nodo. Una malla o lazo es cualquier trayectoria cerrada en un circuito. Un lazo inicia en un nodo, pasa por un conjunto de nodos y retorna al nodo inicial sin pasar por ningún nodo más de una vez. Figura 1. Circuito con nodos, ramas y mallas. Se dice que un lazo es independiente si contiene al menos una rama que no forma parte de ningún otro lazo independiente. Los lazos o trayectorias independientes dan por resultado conjuntos independientes de ecuaciones. Una red con b ramas, n nodos y l lazos independientes satisface el teorema fundamental de la topología de redes: CONEXIÓN DE ELEMENTOS Dos elementos están en serie si comparten exclusivamente un solo nodo y conducen en consecuencia la misma corriente. La conexión serie consta de elementos conectados secuencialmente terminal con terminal. Figura 2. Conexión en serie en un circuito. Dos o más elementos están en paralelo si están conectados a los dos mismos nodos y tienen en consecuencia la misma tensión entre sus terminales. La conexión en paralelo consta de elementos conectados al mismo par de terminales. Sin embargo hay conexiones en donde no se distingue si el elemento esta en serie o en paralelo. Figura 3. Conexión en paralelo en un circuito. PROBLEMAS La Ley de las Corrientes de Kirchhoff, una de las principales leyes de la electricidad utilizada en el análisis de circuitos eléctricos y electrónicos. En este post les voy a explicar como se encuentra las corrientes y los voltajes en un circuito haciendo análisis nodal con la Ley de las Corrientes de Kirchhoff. Lo primero que se necesita para este análisis es conocer qué es un nodo. ¿Qué es un nodo?En un circuito eléctrico, un nodo es un punto donde se cruzan dos o más elementos de circuitos, sea una fuente de voltaje o corriente, resistencias, capacitores, inductores, etc. Para explicar este método usaremos el mismo circuito que usamos en mi anterio post: Ley de los voltajes de Kirchhoff: Método de Mallas En la figura de la parte superior se pueden apreciar los nodos que hemos identificado. Entre la fuente de la izquierda y la resistencia 1 hay un nodo. Lo mismo entre las resistencias R1, R2 y R3. Entre las resistencias R3, R4 y R5. Entre las resistencias R5, R6 y R7. Entre la fuente de la derecha y la resistencia R7. Todos estos elementos van conectados a un nodo en común, el nodo cero, donde se coloca tierra. El propósito del método de nodos es encontrar el voltaje entre todos los nodos y tierra. La diferencia de potencial se produce debido a las caídas de voltaje que le permiten a La Ley de Ohm cumplirse. Pero, en los nodos formados entre resistencias y fuentes ya conocemos el voltaje, es decir, el voltaje de la fuente. En el nodo común, el aterrizado, el voltaje es cero.Para encontrar los voltajes en los nodos 2, 3 y 4 utilizamos el principio fundamental de la Ley de las Corrientes de Kirchhoff: la sumatoria de las corrientes que entran a un nodo es igual a la sumatoria de las corrientes que salen del nodo. Esto no es más que una extensión del Principio de la Conservación de la Energía que es lo que en sí le da su origen a la Ley de Las Corrientes de Kirchhoff. Para saber las corrientes que entran o salen de un nodo, utilizamos la Ley de Ohm. Según la Ley de Ohm, la corriente que pasa por una resistencia es igual a la diferencia de potencial entre la resistividad. I=V/R La diferencia de potencial a la que está sometida una resistencia es igual al voltaje antes de la resistencia menos el voltaje después de la resistencia. Con esto construiremos nuestras ecuaciones para cada nodo. Necesitamos primero escoger el sentido de las corrientes tomando en cuenta que cuando hay una fuente de voltaje la corriente sale del positivo de la fuente. Si no hay una fuente se asume que todas las corrientes fluyen de izquierda a derecha y de arriba hacia abajo. Dicho esto tenemos: Al escoger el sentido de la corriente como lo hemos hecho, es decir, de izquierda a derecha asumimos que los potenciales disminuyen de izquierda a derecha. Ahora procedemos a analizar nodo por nodo. Nodo 2 Como en el Nodo 1 ya conocemos el coltaje (voltaje de la fuente,  voltios) procedemos a analizar el nodo 2.La única corriente que entra al nodo es la que viene de la fuente. La corriente que baja por R2 y por R3 salen del nodo.Vemos que la corriente que entra es la diferencia de voltajes entre la resistencia R1. Se asume que los 10 voltios de la fuente es mayor al voltaje en el nodo 2 ya que se produce una caída de voltaje en la resistencia. Las corrientes que salen serán la corriente que va del nodo 2 al nodo 3 y las que van del nodo 2 a tierra. Se asume que el voltaje 2 es mayor que el voltaje en el nodo 3. El voltaje en tierra es cero voltios. Al final la ecuación es la siguiente:Se trata de igualar la ecuación a cualquier término libre que tengamos. En este caso, el voltaje de la fuente. Nodo 3 Las corrientes que tomamos como salientes en un nodo deben ser tomadas como entrantes en el próximo nodo. La ecuación quedaría de esta forma.Nodo 4 Al nodo 4 entran 2 corrientes y sale una.Una vez más debemos recordar que la corriente sale del positivo de la fuente. El sentido de las flechas indica cuales corrientes entran y cuales salen del nodo.Con esto hemos establecido todas las ecuaciones para los 3 nodos que estamos analizando. Resolviendo el sistema de ecuaciones lineales Siempre que se trabaja con la Ley de las Corrientes de Kirchhoff aparece un sistema de ecuaciones lineales. Luego de establecidas las ecuaciones, se procede a resolver el mismo. Se puede usare cualquier método (reducción, sustitución, determinantes, etc). Yo prefiero utlizar el método de Gauss-Jordan.Se lleva todo a una matriz.Ahora podemos escoger cualquier método para resolver esta matriz.