Física del sonido
Naturaleza del sonido
El sonido consiste en la propagación de una perturbación en un medio (en general el aire).
¿Cómo es la energía sonora? ¿Cómo se propaga la energía de un lugar a otro?
Para comprender mejor esto imaginemos un tubo muy largo lleno de aire. El aire está formado por una cantidad muy grande de pequeñas partículas o moléculas. Inicialmente, el aire dentro del tubo está en reposo (o más técnicamente, en equilibrio). Este equilibrio es dinámico ya que las moléculas se mueven en todas direcciones debido a la agitación térmica, pero con la particularidad de que están homogéneamente distribuidas (en cada cm3 de aire hay aproximadamente la misma cantidad de moléculas - 25 trillones).

Supongamos que se mueve rápidamente el pistón hacia el interior del tubo. Las moléculas que se encuentran junto al pistón serán empujadas, mientras que las que se encuentran alejadas no. En la zona del pistón el aire se encontrará más comprimido que lejos de él, es decir que la misma cantidad de aire ocupa menos espacio. El aire comprimido tiende a descomprimirse (como cuando abrimos la válvula de un neumático) desplazándose hacia la derecha y comprimiendo el aire próximo. Esta nueva compresión implica nuevamente una tendencia a descomprimirse, por lo que la perturbación original se propaga a lo largo del tubo alejándose de la fuente.
Es importante enfatizar que el aire no se mueve de un lugar a otro junto con el sonido. Hay trasmisión de energía pero no traslado de materia (comparar con el olfato).

Propagación
Características del medio - Para que la onda sonora se propague en un medio este debe ser elástico, tener masa e inercia. El aire posee además algunas características relevantes para la propagación del sonido:
- La propagación es lineal (en el intervalo de sonidos audibles la aproximación es válida). Esto permite que diferentes ondas sonoras se propaguen por el mismo espacio al mismo tiempo sin afectarse.

- El medio es no dispersivo. Por esta razón las ondas se propagan a la misma velocidad independientemente de su frecuencia o amplitud.
- El medio es homogéneo. No existen direcciones de propagación privilegiadas por lo que el sonido se propaga esféricamente (en todas direcciones).
Ondas de sonido
Las ondas mecánicas son las que se propagan a través de un material (sólido, líquido, gaseoso). La velocidad de propagación depende de las propiedades elásticas e inerciales del medio. Hay dos tipos básicos de ondas mecánicas: transversales y longitudinales.
En las ondas longitudinales el desplazamiento de las partículas es paralelo a la dirección de propagación, mientras que en las ondas transversales es perpendicular.
Las ondas sonoras son longitudinales. En muchos instrumentos (como en la vibración de una cuerda) podemos identificar ondas transversales (así como en la membrana basilar dentro de la cóclea, en el oído interno).

Excitación periódica
La mayoría de los sonidos de la naturaleza no son producto de una única perturbación del aire, sino de múltiples perturbaciones sucesivas. Un ejemplo de esto es la excitación producida por un diapasón luego de ser golpeado, analizada la clase pasada.
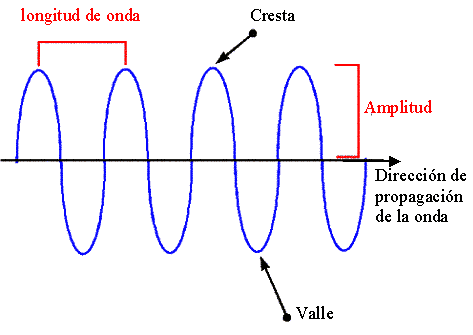
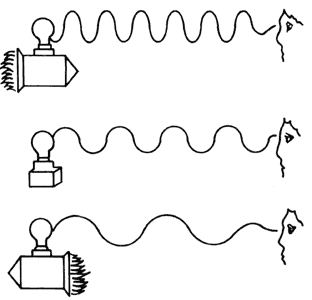
Consideremos un movimiento periódico del pistón. (Ver animación de movimiento periódico del pistón). Sucesión de compresiones y rarefacciones del aire cerca del pistón genera una onda periódica que se propaga alejándose de la fuente. Luego de que la primera perturbación recorrió cierta distancia comienza la segunda, y así sucesivamente. La longitud de onda es la distancia entre perturbaciones sucesivas en el espacio. La frecuencia es la cantidad de perturbaciones por segundo (en ciclos por segundo o Hz).
Como ya mencionamos, al aire libre, las ondas sonoras se propagan en todas direcciones, como ondas esféricas. (Ver animación de radiación de un monopolo y un diapasón). En presencia de superficies reflectoras la onda deja de ser esférica para volverse sumamente compleja debido a la superposición con las reflexiones. Se denomina campo sonoro a la forma en que se distribuye el sonido en diversos puntos dentro de un determinado espacio como una sala o al aire libre.
Se denomina frente de onda al conjunto de puntos de la onda sonora que se encuentran en fase, o de otra forma, una superficie continua que es alcanzada por la perturbación en un instante. Dentro del tubo el frente de onda es plano, mientras que en el monopolo al aire libre el frente de onda es esférico. A determinada distancia las ondas esféricas pueden considerarse ondas planas.
Presión sonora
Según lo visto hasta el momento, el sonido puede considerarse como una sucesión de ondas de compresión y rarefacción que se propaga por el aire. Sin embargo si nos ubicamos en un punto en el espacio (una posición fija) veremos como la presión atmosférica aumenta y disminuye periódicamente a medida que tienen lugar las sucesivas perturbaciones. La presión atmosférica se mide en Pascal y es del orden de los 100.000 Pa (o como en los informes meteorológicos de 100 hPa). Sin embargo, cambios de presión debidos al pasaje de una onda sonora son muy pequeños respecto a este valor de presión atmosférica. Los sonidos más intensos que se perciben implican un incremento de 20 Pa. Por esta razón, para distinguir el incremento de presión de la presión atmosférica en ausencia de sonido se lo denomina presión sonora (p). La presión sonora es la presión que se debe agregar a la presión atmosférica para obtener el valor real de presión atmosférica en presencia de sonido.
Las presiones sonoras audibles varían entre los 20 micro Pa y los 20 Pa (esto se verá mejor en otras clases). Es importante apreciar que es un rango muy importante de variación (de un millón de veces). Esta gran cantidad de cifras es incómoda de manejar. Es por esta razón y por razones fisiológicas que normalmente se expresa la presión sonora en decibles y se denomina Nivel de Presión Sonora (NPS o SPL por sus iniciales en inglés). Se define un nivel de presión sonora de referencia, que es aproximadamente la mínima presión audible (20 micro Pa). Se define el Nivel de Presión Sonora como:

El nivel de referencia corresponde a 0dB mientras que el nivel sonoro máximo corresponde a 120dB. El rango de audición es entonces de 120dB.
| Una sala de conciertos vacía | 30 dB |
| Conversación susurrando | 40 dB |
| Potencia máxima de un altoparlante doméstico | 110 dB |
Dispersión de potencia - pérdida proporcional al cuadrado de la distancia
Representación de una onda sonora
Según la naturaleza del sonido que hemos analizado, su representación en un oscilograma es para un punto espacial, el valor de presión sonora en cada instante de tiempo. Es decir, que la representación más usual de la onda sonora es como la variación de presión sonora en el tiempo. (Hacer diagrama en el pizarrón relacionando la distribución de moléculas y presión en el tubo con la representación del sonido como onda senoidal).
Esta variación de presión sonora puede traducirse a la variación de otra magnitud. Por ejemplo un micrófono es un trasductor de variación de presión sonora a variación de una magnitud eléctrica (voltaje o corriente).
Velocidad, longitud de onda y frecuencia de una onda sonora.
¿De qué forma se relacionan la longitud de onda y la frecuencia de una onda sonora? A mayor frecuencia menor longitud de onda y viceversa. Para ver de que forma se relacionan consideremos una onda periódica desplazándose hacia la derecha. El tiempo entre el instante que una cresta pasa por un punto espacial dado y el instante en que llega la próxima es el período T (T=1/f). La distancia que recorre la onda de un instante a otro corresponde a la longitud de onda L, por lo que la relación es: L /T = Lf = c, donde c es la velocidad del sonido.
Como ya mencionamos la velocidad de propagación del sonido no depende de la frecuencia ni de la intensidad del mismo sino de las características del medio. En el aire su velocidad es de aproximadamente 344 m/s @ 20C (o 1200 km/h - 3 segundos para recorrer 1 km). Esta velocidad aumenta con la temperatura (0.17% /grado C), pero no cambia con la presión. En los líquidos es un poco mayor (1440 m/s en el agua) y mayor aún en los sólidos (5000 m/s en el acero).
No debemos confundir la velocidad de propagación de la onda sonora con la velocidad instantánea de las partículas (estas realizan un movimiento oscilatorio más rápido).
Podemos apreciar que la velocidad del sonido es relativamente alta y normalmente la propagación parece instantánea. Sin embargo en algunos casos es notoria, por ejemplo al compararla con la velocidad de la luz. Ejemplos: ver una banda tocando el la plaza desde lo alto de un edificio, relámpago y trueno, eco, sistema de amplificación.
El rango de frecuencias audibles se considera de forma muy aproximada entre los 20 Hz y 20 kHz. Esto determina cierto rango de valores de longitud de onda del sonido que va desde los 1,7 cm a 17m. Las longitudes de onda son comparables a los objetos ordinarios de la vida cotidiana. Esto es determinante en la forma en que se propaga el sonido, como veremos a continuación.
La longitud de onda juega un papel importante en las dimensiones de los altavoces. Cuando la longitud de onda emitida por un parlante es mucho menor que su propio tamaño la potencia emitida se reduce considerablemente. Es por esta razón que los tweeters son mucho más pequeños que los woofers.
Difracción
Las ondas luminosas poseen una longitud de onda muy pequeña (de 0,6 millonésimos de metros). Sabemos por experiencia que la luz se propaga en línea recta y arroja sombras bien definidas. Por otra parte, las olas del océano tienen una longitud de onda de varios metros. También sabemos que fluyen alrededor de un pilote que sobresalga del agua y son poco afectadas por el mismo. Estos ejemplos ilustran un hecho sumamente importante: las ondas son afectadas por objetos grandes comparados con su longitud de onda. Frente a objetos grandes las ondas arrojan sombras y parecen moverse en línea recta. Pero las ondas son poco afectadas por objetos pequeños comparados con su longitud de onda y pasan a través de tales objetos.
La longitud de onda de las ondas sonoras está a medio camino respecto a los objetos que nos rodean, por lo que en general muestran un comportamiento mixto. Las ondas graves (de longitud de onda grande) son capaces de eludir objetos objetos ordinarios y por ejemplo dar vuelta una esquina. Por el contrario los agudos tienden a propagarse en línea recta y arrojan sombras acústicas. Sabemos por experiencia que los graves de un parlante se dispersan en todas direcciones pero si salimos de la habitación donde está el parlante perdemos las notas agudas.
La difracción es de especial importancia en nuestra capacidad de localización del sonido (para sonidos agudos). La cabeza y las orejas arrojan sombras acústicas.
Otro ejemplo son los micrófonos que arrojan sombra sobre sí mismos para las frecuencias agudas y tiene una transferencia no completamente plana.
Ejercicio: Al aire libre, una persona canta una nota baja y luego silba una nota aguda. El sonido es casi tan intenso adelante y atrás para la nota grave y apreciablemente más fuerte adelante que atrás para el silbido.
Interferencia - Superposición de ondas
Mencionamos que las ondas sonoras se propagan sin afectarse unas a otras, incluso cuando su diferencia de intensidad es muy grande (linealidad del medio). Sin embargo, el sistema auditivo es sensible a la presión sonora total. Es necesario analizar como se combinan o superponen diferentes ondas sonoras. La forma de onda resultante de la superposición de ondas se obtiene sumando algebraicamente cada una de las ondas que componen el movimiento.
Si superponemos ondas sinusoidales de igual frecuencia (pero distinta amplitud y fase) obtenemos una sinusoidal de igual frecuencia pero diferente amplitud y fase. Eventualmente ambas ondas podrían cancelarse, si tuvieran igual amplitud pero a contrafase (180º).

Interferencia constructiva (dfi < L/2) y destructiva (dfi > L/2).
La superposición de sinusoidales es de especial relevancia ya que la teoría de Fourier establece que un sonidos periódico complejo puede descomponerse como suma de sinusoidales.
Reflexión
Cuando una onda sonora se refleja en un plano, parte de la energía se trasmite al obstáculo y otra parte es reflejada. Una de las formas de interferencia más usuales entre dos ondas sonoras es la que se produce entre una onda sonora proveniente de la fuente y una reflexión de la misma que viaja en la misma dirección.
Dos ondas de igual frecuencia viajando en sentidos opuestos forman un patrón de onda estacionaria. La onda resultante no se propaga, sino que oscila presentando puntos de amplitud mínima (nodos) y puntos de amplitud máxima (antinodos). En una cuerda vibrando puede distinguirse un patrón de onda estacionaria.

Pulsaciones
La superposición de ondas de frecuencia cercana produce un fenómeno particular denominado pulsación o batido. Si las frecuencias son muy cercanas el sistema auditivo no es capaz de discriminarlas y se percibe una frecuencia única promedio de las presentes (½ [f1+f2]). La onda resultante cambia en amplitud a una frecuencia igual a la diferencia entre las frecuencias presentes (f1-f2).

Este fenómeno de batido se percibe para diferencias de frecuencia de hasta aproximadamente 15-20 Hz. Al aumentar la diferencia se comienza a percibir un sonido áspero y al seguir aumentando llega un punto en que son percibidas como frecuencias diferentes (Ver ampliación).
Oscilaciones
Si un sistema recibe una única fuerza y comienza a oscilar hasta detenerse, el tipo de oscilación se denomina oscilación libre. Si nada perturbara el sistema este seguiría oscilando indefinidamente. En la naturaleza la fuerza de rozamiento (o fricción) amortigua el movimiento hasta que finalmente se detiene. Este tipo de oscilación se llama oscilación amortiguada y su amplitud varía exponencialmente decayendo con cierta constante de tiempo.

Si se continúa introduciendo energía al sistema podemos contrarrestar la amortiguación logrando una oscilación autosostenida. Esta oscilación se caracteriza por tener además de un ataque y un decaimiento, una fase intermedia casi estacionaria.
Una oscilación forzada puede producirse al aplicar una excitación periódica de frecuencia diferente a la frecuencia propia de oscilación del sistema, logrando que este vibre a la frecuencia de la excitación.

Se denomina generador al elemento que produce la excitación, y resonador al sistema que se pone en vibración. Este tipo de oscilación forzada es la que se produce en las cuerdas de una guitarra que vibran por "simpatía". No siempre es posible obtener una oscilación forzada, sino que depende de la relación entre las características del generador y el resonador.
En el caso de una oscilación forzada, cuando la frecuencia del generador coincide con la del resonador, se dice que el sistema está en resonancia. La magnitud de la oscilación del resonador depende de la magnitud de la excitación pero también de la relación entre las frecuencias de excitación y de resonancia. Cuanto mayor es la diferencia de frecuencias menor será la amplitud de la oscilación. Por el contrario cuando las frecuencias coinciden exactamente una pequeña cantidad de energía de excitación puede producir grandes amplitudes de vibración.
En un caso extremo el sistema resonador puede llegar a romperse, como cuando un cantante rompe una copa de cristal al dar una nota aguda.
Muchos instrumentos musicales tienen un elemento resonador que determina el timbre del instrumento favoreciendo algunos parciales de la excitación original.