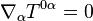Tipos de dilatación
El termino dilatación puede ser interpretado desde diferentes puntos de vista, de esta manera, no existe una definición única para este proceso. Ahora bien, es importante explicar que estas distintas definiciones se establecen en torno al uso que se le vaya a dar. Por ejemplo, puede encontrarse un concepto para el aspecto fisiológico de la palabra como así también para el aspecto vinculado a la físico-química.
De esta manera decimos que, desde la física, el término hace referencia al aumento o incremento en el tamaño de un cuerpo; sin importar el sentido en el que se genere el crecimiento. Es decir, puede prolongarse en longitud, ensancharse, aumentar su volumen o cualquier otra proporción métrica. Pero, lo más importante es que todos estos tipos realizan este proceso mediante un crecimiento de la temperatura, variable según el caso. Es por esto que todos estos tipos pueden considerarse en primer término, de dilatación térmica.
Dilatación térmica: clasificación
- Volumétrica: alude al aumento del volumen de un cuerpo producto de un aumento de temperatura interno. Es una característica necesaria que el objeto tenga una forma geométrica sólida y, como es de suponer, volumen. Debe tenerse en cuenta para esta, el coeficiente correspondiente en este caso (de dilatación volumétrica) y el volumen inicial del cuerpo.
- Superficial: este concepto está íntimamente relacionado con el de dilatación lineal, aquí también un objeto aumenta su tamaño tanto a lo largo como a lo ancho, pero en este caso debe cumplirse la condición fundamental de que el elemento a ser transformado debe ser una superficie plana. Este tipo va a depender principalmente del área inicial que el cuerpo involucre; y estará interrelacionado con el coeficiente de dilatación superficial.
- Lineal: durante este proceso el cuerpo afectado aumenta su tamaño en un sólo sentido, ya sea a lo largo o a lo ancho. No existe ninguna condición especifica necesaria para que la dilatación se clasifique dentro de este tipo, y a su vez, puede ser lineal y de otro tipo nombrado en este articulo. En este caso, el coeficiente utilizado es el llamado: coeficiente de dilatación lineal; y el factor determinante va a ser la longitud inicial del elemento.
- Del agua: esta constituye la excepción al funcionamiento normal de la dilatación de los líquidos (que se contraen disminuyendo su tamaño al dilatarse); cuando el agua elabora este proceso a más de cuatro grados centígrados, aumenta su tamaño y se solidifica. Es así como se da por ejemplo la formación de iceberg y otros fenómenos de congelamiento.
a)dilatacion lineal:cuando el objeto aumenta su longitud
∆Long.= α*∆temp.
siendo α=coeficiente de dilatacion lineal
b)dilatacion superficial:cuando el objeto aumenta su area
∆Area= β*∆temp.
siendo β=coeficiente de dilatacion superficial
c)dilatacion volumetrica:cuado el objeto aumenta su volumen
∆Vol.=γ*∆temp
siendo γ=coeficiente de dialtacion volumetrica
estos coeficientes cumplen una relacion aproximada:
β=2α
γ=3α









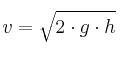
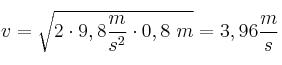
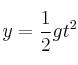 . Como sabemos que la gota comienza a una altura de 0,8 m:
. Como sabemos que la gota comienza a una altura de 0,8 m: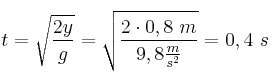
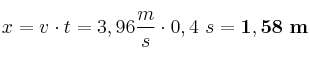





 = velocidad del fluido en la sección considerada.
= velocidad del fluido en la sección considerada. = densidad del fluido.
= densidad del fluido. = presión a lo largo de la línea de corriente.
= presión a lo largo de la línea de corriente. = aceleración gravitatoria
= aceleración gravitatoria = altura en la dirección de la gravedad desde una cota de referencia.
= altura en la dirección de la gravedad desde una cota de referencia. (donde
(donde  ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia
) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia
 , de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.




 es una constante-
es una constante-

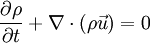
 es la densidad, t el tiempo y
es la densidad, t el tiempo y 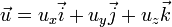 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.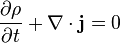
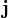 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
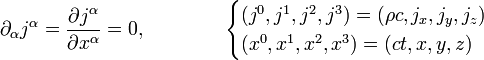
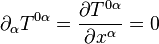
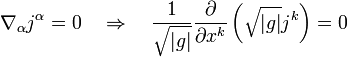
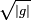 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía: